1.2 Mappings
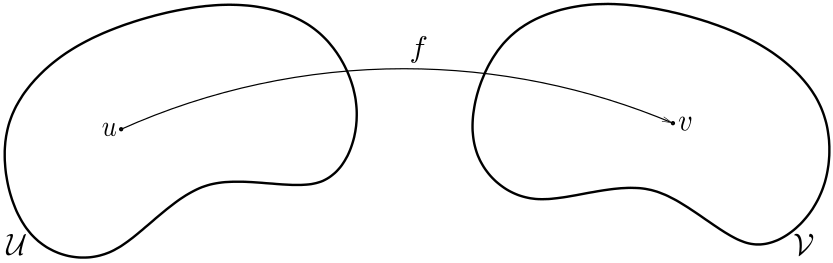
Let $\mathcal{U}, \mathcal{V}$ be two sets and define a mapping $f$ from $\mathcal{U}$ to $\mathcal{V}$ as a rule that assigns to each point $u \in \mathcal{U}$ a unique point $v=f(v) \in \mathcal{V},$ see figure below. The typical notation for a mapping is: $f : \mathcal{U} \rightarrow \mathcal{V}, \mathcal{u} \rightarrow \mathcal{v} = f(u) \in \mathcal{V}.$ In this context, $\mathcal{U}$ is called the domain of $f$ and $\mathcal{V}$ is called the range of $f.$
Suppose we are given two mappings $f : \mathcal{U} \rightarrow \mathcal{V}, u \rightarrow v = f(u)$ and $g : \mathcal{V} \rightarrow \mathcal{W}, v \rightarrow w = g(v),$ the composition mapping $g \circ f$ is defined as $g \circ f: \mathcal{U} \rightarrow \mathcal{W}, u \rightarrow w = g(f(u)),$ as in the next figure below.
